Raspberry Pi RP2040 (Teil 3): Interpolierer - Anwendung gesucht!
AUTOR GÜNTHER WOIGK
In zwei vorangegangenen Blog-Artikeln habe ich mich mit den PIOs - den programmierbaren IO-Einheiten des Raspi RP2040 beschäftigt, die mir trotz ihrer Einschränkungen sehr gut gefallen. Darüber hinaus verfügt aber jeder Rechenkern noch über weitere spezielle Hardware: Eine Integerdivisions-Einheit und zwei Interpolierer. Während die Divisionseinheiten recht unauffällig daher kommen - sie werden automatisch benutzt - muss man mit den Interpolierern selbst interagieren.
Zunächst gilt es herauszufinden, was man mit ihnen eigentlich machen kann:
Ursprünglich entwickelt wurden sie zur Beschleunigung von Audio-Operationen, wofür sie im SDK verwendet werden. Die Dokumentation nennt darüber hinaus Quantisierung, Dithering, Table Lookup Adressberechnung, affine Texture Mapping, Decompression und lineares Feedback. Eine ganze Menge also.
Let's have a look:
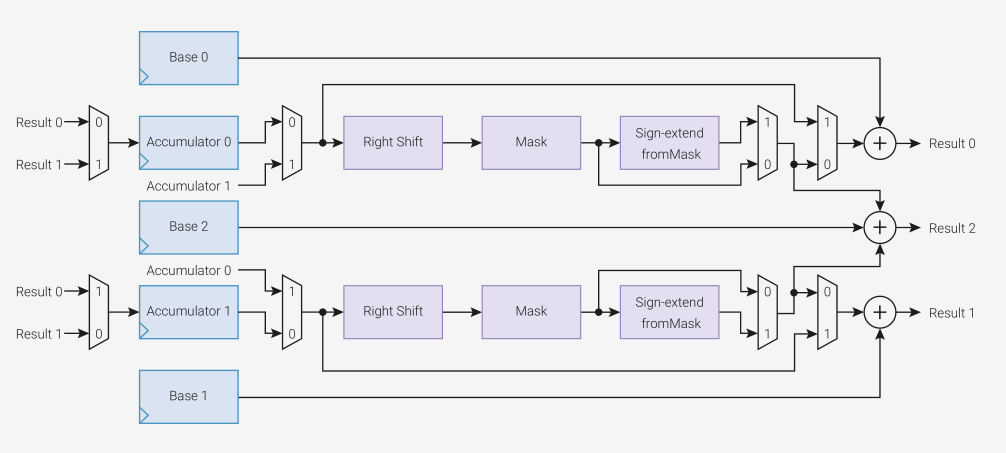
Ähm... wofür ist das denn gut?
Jeder Interpolierer hat zwei Lanes, in denen ein Akkumulatorregister geshiftet und maskiert zu einem Basisregister addiert wird. Das Ergebnis kann ausgelesen und in einen der beiden Akkumulatoren zurückgeladen werden. Man kann auch die Akkumulatorregister beider Lanes, geshiftet und maskiert, zu einer dritten Basis addiert auslesen und in jedem Schritt jeden Akkumulator um 'seine' Basis erhöhen.
Da muss man erst mal drüber meditieren.
Ein denkbares Szenario wäre die Lookup-Adressberechnung für Tabellen, z.B. um in einem textbasierten Bildspeicher je nach Zeichencode und Rasterzeile das Character-ROM zu adressieren. Base2 enthält die Basisadresse des Character-Roms, eine Lane dient zur Erzeugung des Offsets je nach Rasterzeile und die andere den Offset je nach Zeichencode. Die Zeilenadresse wird einmal pro Rasterzeile weitergeschaltet, der Zeichencode für jede Berechnung neu geladen. Das Einschreiben und Auslesen der Register muss die CPU machen, weil die Interpolierer nicht an den allgemeinen Speicherbus angeschlossen sind - DMA ist nicht möglich. In diesem Szenario würde also ein CPU-Kern hauptsächlich den textbasierten Videospeicher auslesen, die Adresse im Character-ROM in einem Takt mittels Interpolierer berechnen und das Grafikbyte in einen DMA-Puffer oder direkt zu einer PIO schreiben, die ein VGA-Signal oder was auch immer ausgibt. Der Interpolierer benötigt zwar nur einen Takt für die Berechnung; insgesamt werden aber doch 2 Takte benötigt, weil die CPU das Register nicht im gleichen Takt schreiben und lesen kann.
Die Frage ist dabei: wieviel Zeit spart das wirklich? Klar ist, die Interpolierer lohnen sich erst, wenn sie für viele Daten in einem Durchgang benutzt werden, weil sonst die Setup-Zeiten jeden Zeitgewinn wieder auffressen.
So oft erfindet man aber die Video-Ausgabe nicht neu, und auch Audio ist im SDK schon abgehandelt, was also geht noch?
Die Interpolierer haben noch zwei spezielle Modi, die interessant klingen: Begrenzen und Interpolieren. (genau!)
Beim Begrenzen (Clamping) werden Eingangswerte auf einen Wertebereich begrenzt. So kann bei der Addition oder Subtraktion zweier Signalwerte das Ergebnis auf den Darstellungsbereich begrenzt werden, zum Beispiel beim Mischen zweier Video- oder Audiosignale. (Sättigungsarithmetik)
Beim Interpolieren wird ein Eingangswert zwischen zwei Stützwerten gemittelt, eine typische Anwendung für Kennfelder.
Beides scheinen sinnvolle Anwendungen zu sein, für die ich auch jeweils einen Anwendungsfall parat habe:
1. Im letzten Artikel benutzte ich eine PIO des RP2040, um einen Laserscanner über ein XY2-100 Interface anzusteuern. Dieses benutzt uint16 Werte. Die X- und Y-Koordinaten müssen deshalb auf diesen Bereich begrenzt werden, bevor sie zum Scanner gesendet werden. Die oberen Bits werden sonst schlicht nicht gesendet und im Bereich der unteren Bits kommt es zum Wrap-around, was den Scanner in seinem Scanfeld hin- und herjagen würde. Da versuche ich doch mal, die Werte mit dem Interpolierer zu begrenzen.
2. Laserscanner haben eine inhärente Geometrieverzerrung: Sie projizieren oft nicht frontal auf ihr Beschriftungsziel und der Strahl wird mit einer Linse fokussiert, die optische Verzerrungen mit sich bringt. All das wird über eine zweidimensionale Korrekturtabelle vorab kompensiert. Der ideale Anwendungsfall für eine Interpolation - sogar eine zweidimensionale! 😃
Let's Go!
Alle Codebeispiele können auf godbolt.org ausprobiert werden. Bei den einzelnen Tests gebe ich immer einen Link an; man kann den Source aber auch selbst hochladen. Dabei muss man aber auch den richtigen Compiler mit den richtigen Optionen angeben. Es ist natürlich auch interessant, unterschiedliche Compiler und CPUs miteinander zu vergleichen.
Der RP2040 hat einen ARM CortexM0+:
- Compiler: ARM gcc 9.2.1 (none)
- Optionen: -march=armv6-m -mcpu=cortex-m0plus -mthumb -O2
Die Codebeispiele haben alle die folgenden Definitionen vorangestellt.
Diese werde ich im Folgenden nicht jedesmal wiederholen:
#include <stdint.h>
// Utilities:
#define LIKELY(x) __builtin_expect((x),true)
#define UNLIKELY(x) __builtin_expect((x),false)
template<typename S, typename T, typename U>
static inline T limit (S _min, T _val, U _max) {
return _val >= _min ? _val <= _max ? _val : _max : _min;
}
// Externe Funktionen: (hier nicht implementiert)
extern void pio_put_x(uint32_t);
extern void pio_put_y(uint32_t);
// Benötigte Definitionen aus dem Pico-SDK:
#define SIO_BASE 0xd0000000
#define SIO_INTERP0_ACCUM0_OFFSET 0x00000080
typedef volatile uint32_t io_wo_32;
typedef volatile uint32_t io_rw_32;
typedef const volatile uint32_t io_ro_32;
typedef struct {
io_rw_32 accum[2];
io_rw_32 base[3];
io_ro_32 pop[3];
io_ro_32 peek[3];
io_rw_32 ctrl[2];
io_rw_32 add_raw[2];
io_wo_32 base01;
} interp_hw_t;
#define interp_hw_array ((interp_hw_t *)(SIO_BASE + SIO_INTERP0_ACCUM0_OFFSET))
#define interp0_hw (&interp_hw_array[0])
#define interp1_hw (&interp_hw_array[1])
#define interp0 interp0_hw
#define interp1 interp1_hw
// Convenience:
using int32 = int32_t;
using uint32 = uint32_t;
using uint = unsigned int;
Clamping - Werte auf einen Bereich begrenzen
Zum Vergleich möchte ich meinen bestehenden Code so umbauen, dass er einmal mit reiner CPU-Arithmetik und einmal mit dem Interpolierer etwa das gleiche macht.
Der reine CPU-Code zum Aufbereiten und Senden der Scannerkoordinaten sah bisher wie folgt aus:
void pio_send_data (float x, float y)
{
x = limit(-0x8000, x, 0x7fff);
y = limit(-0x7fff, y, 0x8000); // Y axis inverted
pio_put( 0x8000 + int(x), 0x8000 - int(y) );
}
Die Fließkomma-Koordinaten wurden bisher als Float limitiert, womit auch extreme Überschüsse, z.B. bei verbockten 3D-Berechnungen erfasst würden. Da der Interpolierer nur mit 32-Bit Integerwerten arbeitet, muss das als erstes angepasst werden. Die Begrenzung der 16-Bit Koordianten im 32-Bit-Bereich erlaubt ja auch noch extreme Überschwinger. Um den Code-Vergleich nicht mit der Float-to-Integer Konvertierung aufzublähen, übernimmt die Funktion jetzt int32 Werte:
void pio_send_data (int32_t x, int32_t y)
{
pio_put_x( limit(0, 0x8000+x, 0xffff) );
pio_put_y( limit(0, 0x8000-y, 0xffff) );
}
Die Version mit Interpolierer sieht so aus:
void pio_send_data (int32_t x, int32_t y)
{
interp1->accum[0] = 0x8000+x;
pio_put_x( interp1->peek[0] );
interp1->accum[0] = 0x8000-y;
pio_put_y( interp1->peek[0] );
}
Der Interpolierer musste vorher einmalig initialisiert werden und sollte dann auch nur für diese Aufgabe verwendet werden. Die Namensgebung für die verschiedenen zu konfigurierenden Switches ist etwas eigen:
void init_interpolator1_for_clamping()
{
static constexpr uint32_t SCANNER_MIN = 0;
static constexpr uint32_t SCANNER_MAX = 0xffff;
interp_config icfg = interp_default_config();
interp_config_set_clamp(&icfg, true); // select clamping mode [base0 .. base1]
interp_config_set_cross_input(&icfg,false); // lane0 input from accu0
interp_config_set_signed(&icfg, true); // select signed compare
interp_config_set_add_raw(&icfg,true); // bypass shift+mask
interp_set_config(interp1, 0/*lane*/, &icfg);
interp1->base[0] = SCANNER_MIN; // lower limit
interp1->base[1] = SCANNER_MAX; // upper limit
}
Betrachten wir als erstes die reine CPU-Version von pio_send_data() auf godbolt.org:
https://godbolt.org/z/Y11nP4TeM
Auch wer nicht fließend in ARM-Assembler ist, kann daraus wertvolle Informationen saugen. Die meisten Befehle werden beim Cortex-M0 in 1 bis 2 Takten abgearbeitet, man kann von der Codelänge also in etwa auf die Ausführungszeit schließen. Dabei ist es vor Allem wichtig, Sprünge zu erkennen und richtig einzuordnen. Sprünge sind alle Assemblerbefehle, die mit 'b' wie 'branch' anfangen. godbolt hilft mit Tooltips mit Erklärungen zu den Assemblerbefehlen, wenn man mit dem Mauszeiger über einer Assemblerzeile schwebt.
Das Ergebnis für den reinen CPU-Code ist schon etwas länglich:
pio_send_data(long, long):
movs r3, #128
lsls r3, r3, #8
mov ip, r3
movs r3, #128
add r0, r0, ip
push {r4, lr}
lsls r3, r3, #9
movs r4, r1
cmp r0, r3
blt .L2
ldr r0, .L7
.L3: bl pio_put_x(unsigned long)
movs r0, #128
movs r3, #128
lsls r0, r0, #8
subs r0, r0, r4
lsls r3, r3, #9
cmp r0, r3
blt .L4
ldr r0, .L7
.L5: bl pio_put_y(unsigned long)
pop {r4, pc}
.L2: mvns r3, r0
asrs r3, r3, #31
ands r0, r3
b .L3
.L4: mvns r3, r0
asrs r3, r3, #31
ands r0, r3
b .L5
.L7: .word 65535
Kurz vor .L3 gibt es ein bedingtes Schleifchen nach .L2 und vor .L5 eins nach .L4. Diese Wege nimmt der Code, wenn limit() einen Wert begrenzt. Eigentlich müssten 4 solche Verzweigungen da sein, da limit() zweimal aufgerufen wird und jeweils zwei Vergleiche enthält, aber der Compiler kennt einen Trick, zumindest einen der Ausdrücke ohne Weiche hinzubekommen. Solche Tricks sind wertvoll, weil jede Verzweigung die CPU Zeit kostet, weil dann vorausschauend geladener Code verworfen werden muss.
Interessant sind die 22 Zeilen bis .L2 exclusive. Die Zweige bei .L2 und .L4 werden nur abgearbeitet, wenn tatsächlich begrenzt wird, also hoffentlich nie. 😃
Zum Vergleich jetzt die Version mit Hilfe des Interpolierers.
https://godbolt.org/z/YW7EG9dWh
pio_send_data(long, long):
movs r3, #128
lsls r3, r3, #8
mov ip, r3
push {r4, r5, r6, lr}
ldr r4, .L3
add r0, r0, ip
str r0, [r4]
ldr r0, [r4, #32]
movs r5, r1
bl pio_put_x(unsigned long)
movs r3, #128
lsls r3, r3, #8
subs r3, r3, r5
str r3, [r4]
ldr r0, [r4, #32]
bl pio_put_y(unsigned long)
pop {r4, r5, r6, pc}
.L3: .word -805306176
Das sind nur 17 Zeilen im Vergleich zu den 22 Zeilen im Hauptzweig der reinen CPU-Lösung. Das sollte also tatsächlich schneller gehen, auch wenn der Code mehr Register auf den Stack schiebt.
Die schlechte Nachricht ist aber: Während die Hardware-Lösung so weitgehend ausgereizt ist, lässt sich die Softwarelösung in diesem Fall noch optimieren. Und bevor wir eine proprietäre und begrenzte Ressource im RP2040 benutzen, versuchen wir doch erst einmal die reine CPU-Lösung auszureizen:
Die Grenzwerte für den Laserscanner sind keine beliebigen Werte sondern decken exakt den Bereich von 2^16 ab. Damit können wir eine Grenzwertüberschreitung in positiver und negativer Richtung daran erkennen, dass Bits jenseits dieser 16 Bit gesetzt sind:
https://godbolt.org/z/qc9Kd65cc
void pio_send_data (int32_t x, int32_t y)
{
x = 0x8000 + x;
y = 0x8000 - y;
if (UNLIKELY(uint32_t(x)>>16)) x = x<0 ? 0 : 0xffff;
if (UNLIKELY(uint32_t(y)>>16)) y = y<0 ? 0 : 0xffff;
pio_put_x(x);
pio_put_y(y);
}
erzeugter Code:
pio_send_data(long, long):
movs r3, #128
lsls r3, r3, #8
mov ip, r3
push {r4, lr}
movs r4, #128
add r0, r0, ip
lsls r4, r4, #8
subs r4, r4, r1
lsrs r3, r0, #16
bne .L13
lsrs r3, r4, #16
bne .L14
.L3: bl pio_put_x(unsigned long)
movs r0, r4
bl pio_put_y(unsigned long)
pop {r4, pc}
.L13: mvns r0, r0
asrs r0, r0, #31
lsls r0, r0, #16
lsrs r0, r0, #16
lsrs r3, r4, #16
beq .L3
.L14: mvns r4, r4
asrs r4, r4, #31
lsls r4, r4, #16
lsrs r4, r4, #16
b .L3
Das sind jetzt sogar nur noch 16 Zeilen im Hauptzweig und es werden auch noch weniger Register auf den Stack gepusht. Vermutlich ist das jetzt schneller...UNLIKELY() ist ein Hinweis für den Compiler, dass dies der unwahrscheinlichere Pfad ist, und er den Code-Fluss für den anderen Fall optimieren soll. Dadurch wird hier der wahrscheinlichere Pfad ohne Sprung durchlaufen.
Die Shifterei, die der Compiler bei .L13 und .L14 erzeugt, um aus dem Vorzeichenbit eine 0 oder eine 0xffff zu machen, ist übrigens auch ganz interessant. 😃
Die Erkenntnis ist jedenfalls, dass sich der Interpolierer zum Clampen nur lohnt, wenn auf krumme Werte begrenzt werden muss oder wenn man größere Datenmengen in einem Rutsch bearbeiten kann. Dann kann man die beiden Registeradressen des Interpolierers in zwei Register der CPU laden und hat diese Setup-Zeiten nur einmal. In unserem Fall haben wir aber immer nur zwei Werte - immerhin. Es hätte ja auch nur einer sein können. 😄
Interpolieren - zwischen Stützpunkten in einem Kennfeld vermitteln
Im zweiten Versuch baue ich in mein Laserscanner-Projekt eine optische Korrektur mittels zweidimensionaler Korrekturtabelle ein. Dass ich dafür keine realen Werten habe, ist hierbei egal. Ich fülle die Tabelle einfach so, dass das Ergebnis mit dem Input identisch sein sollte. Wenn was nicht funktioniert, sieht man es so sofort am erzeugten Bild.
Die Korrekturtabelle soll 64 x 64 Werte umfassen, genauer gesagt 65 x 65, denn 64 Abschnitte haben zusammen genommen 65 Enden. diese Größe ergibt sich nicht von ungefähr: Einmal sollte sie 2^n Abschnitte haben, damit man mit Bit-Shiften und Maskieren statt Division und Rest arbeiten kann. Für die Interpolierer-Lösung muss sie das sogar sein, denn der kann nicht anders. Die Größe ergibt sich aus einer Kosten-Nutzen-Abschätzung: Bei 64x64 belegt die Tabelle für 65*65 Einträge mit je zwei int16 Koordinaten 16900 Bytes. Der nächste Schritt wäre 128x128, was schon knapp 68 kB belegen würde. Das wäre noch zu überlegen. Aber für den Codevergleich ist das egal. Auch die Unterteilung in 2x2 Bereiche würde sich in der Berechnung nicht von 64x64 unterscheiden, sie wäre halt nur ... ziemlich ungenau.
Der Aufruf des Interpolierers sieht in beiden Fällen so aus:
#define XY2_MAP_BITS 6 // 6 bits for the map: 2^6 = 64
#define XY2_LOW_BITS 10 // remainder used to interpolate: 6+10 bits = scan field width
void pio_send_data (int32_t x, int32_t y)
{
Point2D p{uint32_t(0x8000+x), uint32_t(0x8000-y)};
p = map2D<XY2_MAP_BITS,XY2_LOW_BITS>(p,map);
pio_put_x(p.x);
pio_put_y(p.y);
}
Die Implementierung von map2D() ist für beide Versionen ebenfalls noch einheitlich; erst die darin aufgerufene Funktion interpolate() ist unterschiedlich. Der folgende Code ist auch noch nicht ganz vollständig. Der vollständige Code ist in den godbolt-Beispielen ersichtlich.
Für eine 2D-Interpolierung muss dreimal zwischen zwei Punkten mit jeweils zwei Koordinaten interpoliert werden. Das macht zusammen 6 Aufrufe des Interpolierers:
template<uint map_bits=6, uint bits=10>
Point2D map2D (Point2D p, Point2D map[])
{
clamp<map_bits+bits>(p);
uint32 ix = p.x >> bits;
uint32 iy = p.y >> bits;
// interpolate P(0,0) - P(1,0)
map += ix + iy + (iy << map_bits); // ix + iy*(2^map_bits+1)
Point2D p1 = interpolate<bits>(p.x, map[0], map[1]);
// interpolate P(0,1) - P(1,1)
map += 1 + (1<<map_bits);
Point2D p2 = interpolate<bits>(p.x, map[0], map[1]);
// interpolate vertically:
return interpolate<bits>(p.y, p1, p2);
}
Zum Interpolieren wird zwischen zwei Stützpunkten mit einem Blendfaktor alpha im Bereich [0..[1 gemittelt. Um Integerrechnung oder den Interpolierer benutzen zu können, ist alpha auf <bits> skaliert.
#if XY2_USE_MAP_PICO_INTERP
template<uint bits> inline Point2D interpolate (uint a, Point2D Pi, Point2D Pj)
{
// The RP2040 interpolator actually always uses 8 bits precision.
// The interpolator must have been setup before!
interp0->accum[1] = a; // alpha needs only be loaded once for x and y
interp0->base[0] = Pi.x;
interp0->base[1] = Pj.x;
Pi.x = interp0->peek[1]; // lane 1 returns the interpolation
interp0->base[0] = Pi.y;
interp0->base[1] = Pj.y;
Pi.y = interp0->peek[1];
return Pi;
}
#else
template<uint bits> inline Point2D interpolate (uint a, Point2D Pi, Point2D Pj)
{
a &= mask<bits>;
Pi.x += ((Pj.x-Pi.x) * a) >> bits;
Pi.y += ((Pj.y-Pi.y) * a) >> bits;
return Pi;
}
#endif
Der Setup-Code für den Interpolierer:
interp_config cfg = interp_default_config();
interp_config_set_blend(&cfg, true);
interp_set_config(interp0, 0, &cfg); // reset lane 0
cfg = interp_default_config();
interp_config_set_shift(&cfg,(XY2_LOW_BITS-8)&31); // right shift!
interp_config_set_mask(&cfg,0,7);
interp_config_set_signed(&cfg, true);
interp_set_config(interp0, 1, &cfg);
Hier wieder der Link auf godbolt:
https://godbolt.org/z/Y3K4YWsrd
Das Code-Beispiel ist voreingestellt für den Pico-Interpolierer, in Zeile 45 ist der Switch um auf die CPU-Lösung umzuschalten. Ich habe den Aufruf von clamp() in Zeile 91 auskommentiert, um das Beispiel einfach zu halten.
Die reine CPU-Lösung hat 63 Assemblerbefehle und die Lösung mit Interpolierer 66 Assemblerbefehle. Das sieht für den Interpolierer auch nicht gut aus.
Um reale Ergebnisse zu erhalten, habe ich dann beide Versionen in meinem Laser-Projekt gemessen. Über das XY2-Interface werden 100.000 Punkte pro Sekunde ausgegeben, das entspricht 600.000 Interpolierungen. Die folgende Tabelle zeigt die CPU-Last für 3 Demos jeweils ohne, mit CPU-Arithmetik und mit Pico-Interpolierer:
| Demo | ohne | CPU | Pico |
| Checker board | 38.8% | 45.3% | 45.4% |
| analog Clock | 39.4% | 46.1% | 46.0% |
| Lissajous | 54.3% | 60.7% | 60.6% |
Fazit:
Interpolieren mit reiner CPU-Arithmetik oder mit Pico Interpolierer ist praktisch gleich schnell.
Die zusätzliche CPU-Last ist bei 125MHz etwa 6.6 Prozentpunkte, oder etwa 8.25 MHz.
Wie beim Begrenzen bringt die Interpoliereinheit nur Vorteile, wenn man große Datenmengen am Stück durchschieben kann, weil dann einige Setup-Zeiten nur einmal anfallen. Viel kann man dabei aber nicht sparen, da man nicht darum herum kommt, für jede Interpolierung die zugehörigen zwei Stützwerte und den Blendfaktor in die Register zu schreiben.
Der Pico-Interpolierer hat den Vorteil, dass er intern mit 40 Bit rechnet und so für die Stützpunkte einen größeren Wertebereich ermöglicht. Allerdings hat er zwischen den Stützpunkten nur eine Auflösung von 8 Bit, also maximal 256 unterschiedliche Werte.
Demgegenüber rechnet die CPU nativ nur mit 32 Bit, hat aber in unserem Fall eine Auflösung zwischen den Stützpunkten von 10 Bit, also 1024 unterschiedliche Werte; und kommt natürlich ohne diese Spezialhardware aus.
Zum Autor
Günter Woigk arbeitet als Software Developer im Embedded-Bereich der Mathema GmbH mit dem Schwerpunkt auf C und C++ Programmierung. Momentan interessiert er sich für die Möglichkeiten, die der neue Ansatz im RP2040 für kommerzielle Entwicklungen bietet.







